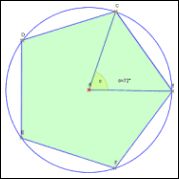
Das Problem der Konstruierbarkeit regelmäßiger Vielecke mit Zirkel und Lineal war lange Zeit ungelöst. Erst Carl Friedrich Gauß bewies, dass ein reguläres n-Eck genau dann konstruierbar ist, wenn die Zahl n das Produkt einer Zweierpotenz und von verschiedenen Fermatschen Primzahlen ist, d. h. Primzahlen der Form
![]()
Es sind folgende Fermatsche Primzahlen bekannt:
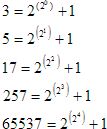
Das heißt konkret, dass außer dem Quadrat die regulären n-Ecke für n = 3, 5, 17, 257, 65537 einschließlich aller möglichen Verdoppelungen und Produkte konstruierbar sind. Die Konstruktion des 17-Ecks wurde von Gauß selbst durchgeführt.
Im Folgenden soll die Konstruktion des regulären Fünfecks dargestellt werden. Dazu teilt man die Strecke [AB] im Verhältnis des Goldenen Schnitts, d. h. für den Teilpunkt T gilt:
![]()
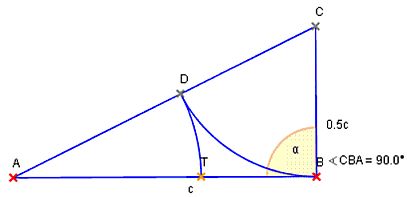
Das gleichschenklige Dreieck ATS heißt goldenes Dreieck, weil das Verhältnis von Schenkellänge und Basislänge den Wert hat. Der Winkel an der Spitze eines Goldenen Dreiecks beträgt 36°, die Größe der Basiswinkel demzufolge 72°.
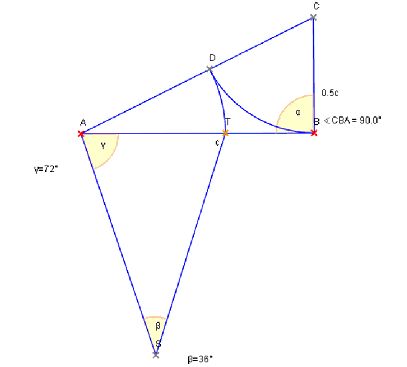
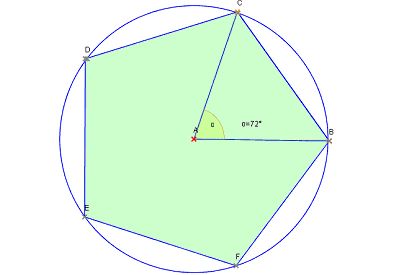
Durch fortlaufendes Abtragen der zum Mittelpunktswinkel 72° gehörenden Kreissehne erhält man schließlich das reguläre Fünfeck.
StD Reimund Hetterich
